一、插入排序
算法思想:
利用顺序查找实现“在 R[1..i-1]中查找 R[i]的插入位置”的插入排序。
算法描述:
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
- 1.从第一个元素开始,该元素可以认为已经被排序
- 2.取出下一个元素,在已经排序的元素序列中从后向前扫描
- 3.如果该元素(已排序)大于新元素,将该元素移到下一位置
- 4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 5.将新元素插入到该位置后
- 6.重复步骤2~5
- 算法演示:

算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void insertion_sort(int array[], int first, int last) { int i,j; int temp; for (i = first+1; i<=last;i++) { temp = array[i]; j=i-1; //與已排序的數逐一比較,大於temp時,該數向後移 while((j>=first) && (array[j] > temp)) { array[j+1] = array[j]; j--; } array[j+1] = temp; //被排序数放到正确的位置 } } |
二、冒泡排序
算法思想:
将被排序的记录数组R[1..n]垂直排列,每个记录R[i]看作是重量为R[i].key的气泡。根据轻气泡不能在重气泡之下的原则,从下往上扫描数组R:凡扫描到违反本原则的轻气泡,就使其向上”飘浮”。如此反复进行,直到最后任何两个气泡都是轻者在上,重者在下为止。(不管轻者在上,还是重者在上,原理都一样)
算法描述:
- 1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
- 2.对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
- 3.针对所有的元素重复以上的步骤,除了最后一个。
- 4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
- 算法图示:
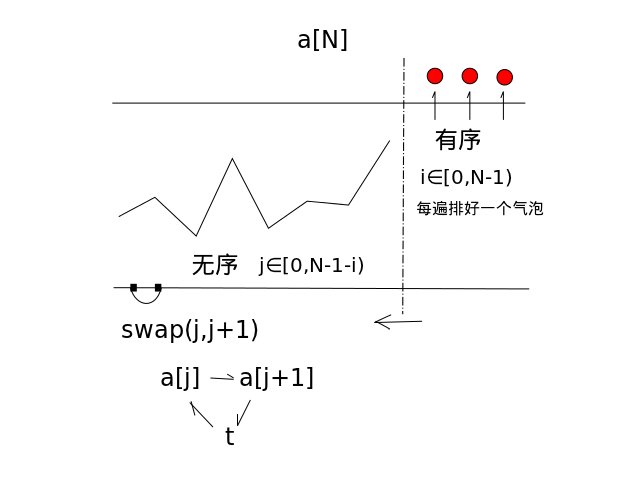
算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #include <stdio.h> #define LENGTH 8 void main() { int i, j, tmp, number[LENGTH] = {95, 45, 15, 78, 84, 51, 24, 12}; for (i = 0; i < LENGTH; i++) { for (j = LENGTH - 1; j > i; j--) { if (number[j] < number[j-1]) { tmp = number[j-1]; number[j-1] = number[j]; number[j] = tmp; } } } for (i = 0; i < LENGTH; i++) { printf("%d ", number[i]); } printf("\n"); } |
三、选择排序
算法描述:
比如在一个长度为N的无序数组中,在第一趟遍历N个数据,找出其中最小的数值与第一个元素交换,第二趟遍历剩下的N-1个数据,找出其中最小的数值与第二个元素交换……第N-1趟遍历剩下的2个数据,找出其中最小的数值与第N-1个元素交换,至此选择排序完成。
算法图示:
算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | //交换data1和data2所指向的整形 void DataSwap(int* data1, int* data2) { int temp = *data1; *data1 = *data2; *data2 = temp; } /******************************************************** *函数名称:SelectionSort *参数说明:pDataArray 无序数组; * iDataNum为无序数据个数 *说明: 选择排序 *********************************************************/ void SelectionSort(int* pDataArray, int iDataNum) { for (int i = 0; i < iDataNum - 1; i++) //从第一个位置开始 { int index = i; for (int j = i + 1; j < iDataNum; j++) //寻找最小的数据索引 if (pDataArray[j] < pDataArray[index]) index = j; if (index != i) //如果最小数位置变化则交换 DataSwap(&pDataArray[index], &pDataArray[i]); } } |
四、快速排序
算法思想:找一个记录,以它的关键字作为“枢轴”,凡其关键字小于枢轴的记录均移动至该记录之前,反之,凡关键字大于枢轴的记录均移动至该记录之后。致使一趟排序之后,记录的无序序列 R[s..t]将分割成两部分:R[s..i-1]和R[i+1..t],
且 R[j].key≤ R[i].key ≤ R[t].key (s≤j≤i-1) 枢轴(i+1≤j≤t)。
算法描述:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
3.再对左右区间重复第二步,直到各区间只有一个数。
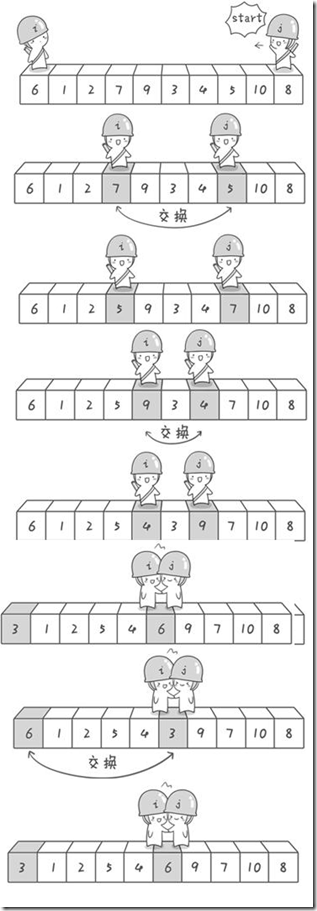
算法图示:
6 1 2 7 9 3 4 5 10 8
分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。首先哨兵j开始出动。因为此处设置的基准数是最左边的数,所以需要让哨兵j先出动,这一点非常重要(请自己想一想为什么)。哨兵j一步一步地向左挪动(即j–),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。现在交换哨兵i和哨兵j所指向的元素的值。直到哨兵i和哨兵j相遇了,哨兵i和哨兵j都走到3面前。说明此时“探测”结束。我们将基准数6和3进行交换。
细心的同学可能已经发现,快速排序的每一轮处理其实就是将这一轮的基准数归位,直到所有的数都归位为止,排序就结束了。下面上个霸气的图来描述下整个算法的处理过程。

算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | #include <stdio.h> int a[101],n;//定义全局变量,这两个变量需要在子函数中使用 void quicksort(int left,int right) { int i,j,t,temp; if(left>right) return; temp=a[left]; //temp中存的就是基准数 i=left; j=right; while(i!=j) { //顺序很重要,要先从右边开始找 while(a[j]>=temp && i<j) j--; //再找右边的 while(a[i]<=temp && i<j) i++; //交换两个数在数组中的位置 if(i<j) { t=a[i]; a[i]=a[j]; a[j]=t; } } //最终将基准数归位 a[left]=a[i]; a[i]=temp; quicksort(left,i-1);//继续处理左边的,这里是一个递归的过程 quicksort(i+1,right);//继续处理右边的 ,这里是一个递归的过程 } int main() { int i,j,t; //读入数据 scanf("%d",&n); for(i=1;i<=n;i++) scanf("%d",&a[i]); quicksort(1,n); //快速排序调用 //输出排序后的结果 for(i=1;i<=n;i++) printf("%d ",a[i]); getchar();getchar(); return 0; } |
五、堆排序
算法思想:
堆的定义:堆是满足下列性质的数列{r1, r2, …,rn}:
若将此数列看成是一棵完全二叉树,则堆或是空树或是满足下列特性的完全二叉树:其左、右子树分别是堆,并且当左/右子树不空时,根结点的值小于(或大于)左/右子树根结点的值。由此,若上述数列是堆,则 r1 必是数列中的最小值或最大值,分别称作小顶堆或大顶堆。
堆排序:即是利用堆的特性对记录序列进行排序的一种排序方法。
堆排序思想:
先建一个“大顶堆”,即先选得一个关键字为最大的记录,然后与序列中最后一个记录 交换,之后继续对序列中前 n-1 记录进行“筛选”,重新将它调整为一个“大顶堆”再 将堆顶记录和第 n-1 个记录交换,如此反复直至排序结束。所谓“筛选”指的是对一棵 左/右子树均为堆的完全二叉树,“调整”根结点使整个二叉树为堆。堆排序的特点:在以后各趟的“选择”中,利用在第一趟选择中已经得到的关键字比较的结果。
堆的操作:
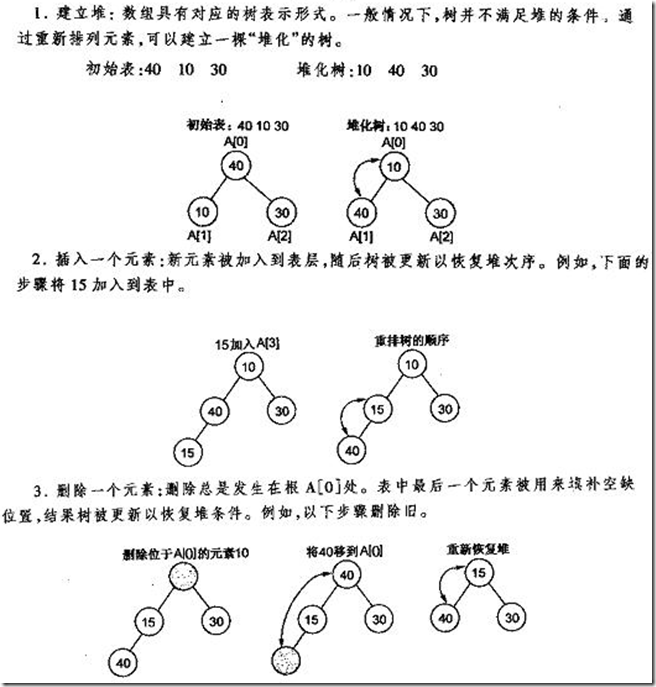
堆化数组:
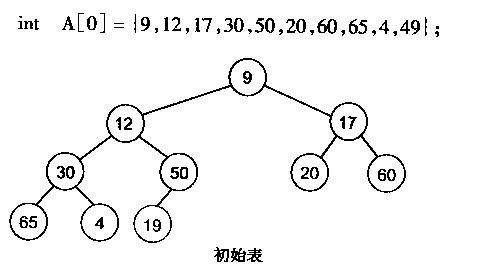
很明显,对叶子结点来说,可以认为它已经是一个合法的堆了即20,60, 65, 4, 49都分别是一个合法的堆。只要从A[4]=50开始向下调整就可以了。然后再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分别作一次向下调整操作就可以了。下图展示了这些步骤:
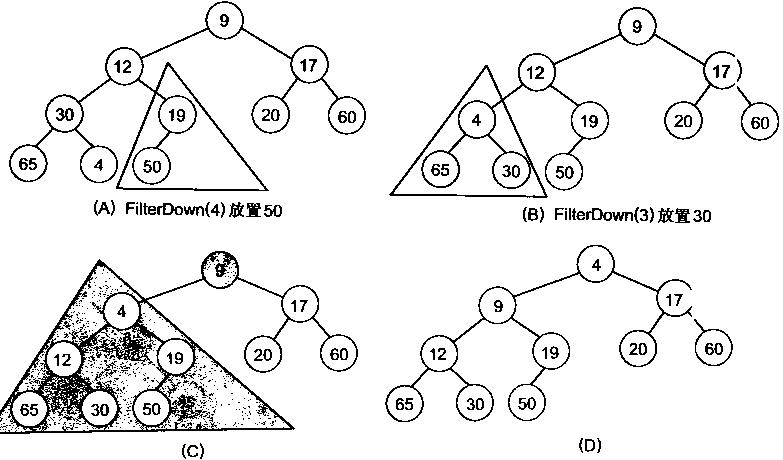
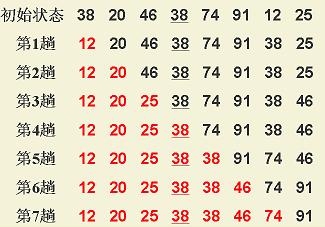
堆排序演示图:

算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 | #include <iostream> using namespace std; /* #堆排序#% #数组实现#% */ //#筛选算法#% void sift(int d[], int ind, int len) { //#置i为要筛选的节点#% int i = ind; //#c中保存i节点的左孩子#% int c = i * 2 + 1; //#+1的目的就是为了解决节点从0开始而他的左孩子一直为0的问题#% while(c < len)//#未筛选到叶子节点#% { //#如果要筛选的节点既有左孩子又有右孩子并且左孩子值小于右孩子#% //#从二者中选出较大的并记录#% if(c + 1 < len && d[c] < d[c + 1]) c++; //#如果要筛选的节点中的值大于左右孩子的较大者则退出#% if(d[i] > d[c]) break; else { //#交换#% int t = d[c]; d[c] = d[i]; d[i] = t; // //#重置要筛选的节点和要筛选的左孩子#% i = c; c = 2 * i + 1; } } return; } void heap_sort(int d[], int n) { //#初始化建堆, i从最后一个非叶子节点开始#% for(int i = (n - 2) / 2; i >= 0; i--) sift(d, i, n); for(int j = 0; j < n; j++) { //#交换#% int t = d[0]; d[0] = d[n - j - 1]; d[n - j - 1] = t; //#筛选编号为0 #% sift(d, 0, n - j - 1); } } int main() { int a[] = {3, 5, 3, 6, 4, 7, 5, 7, 4}; //#QQ#% heap_sort(a, sizeof(a) / sizeof(*a)); for(int i = 0; i < sizeof(a) / sizeof(*a); i++) { cout << a[i] << ' '; } cout << endl; return 0; } |
六、归并排序
算法思想:
将两个或两个以上的有序子序列“归并”为一个有序序列,是一种稳定的排序方法。在内部排序中,通常采用的是 2-路归并排
序。即将两个位置相邻的有序子序列,归并为一个有序序列
算法描述:
- 1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 2.设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 4.重复步骤3直到某一指针到达序列尾
- 5.将另一序列剩下的所有元素直接复制到合并序列尾
算法代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 | //#只完成兩段之間歸併的功能#% void Merge(int a[], int b[], int low, int mid, int high) { int k = low; int begin1 = low; int end1 = mid; int begin2 = mid + 1; int end2 = high; while(k <= high ) { if(begin1 > end1) b[k++] = a[begin2++]; else if(begin2 > end2) b[k++] = a[begin1++]; else { if(a[begin1] <= a[begin2]) b[k++] = a[begin1++]; else b[k++] = a[begin2++]; } } } void MergePass(int a[], int b[], int seg, int size) { int seg_start_ind = 0; while(seg_start_ind <= size - 2 * seg) //#size - 2 * seg的意思是滿足可兩兩歸併的最低臨界值#% { Merge(a, b, seg_start_ind, seg_start_ind + seg - 1, seg_start_ind + seg * 2 - 1); seg_start_ind += 2 * seg; } //#如果一段是正好可歸併的數量而另一段則少於正好可歸併的數量#% if(seg_start_ind + seg < size) Merge(a, b, seg_start_ind, seg_start_ind + seg - 1, size - 1); else for(int j = seg_start_ind; j < size; j++) //#如果只剩下一段或者更少的數量#% b[j] = a[j]; } void MergeSort(int a[], int size) { int* temp = new int[size]; int seg = 1; while(seg < size) { MergePass(a, temp, seg, size); seg += seg; MergePass(temp, a, seg, size); seg += seg; } delete [] temp; } int main() { int a[] = {3, 5, 3, 6, 4, 7, 5, 7, 4}; MergeSort(a, sizeof(a) / sizeof(*a)); //#輸出#% for(int i = 0; i < sizeof(a) / sizeof(*a); i++) cout << a[i] << ' '; cout << endl; return 0; } |
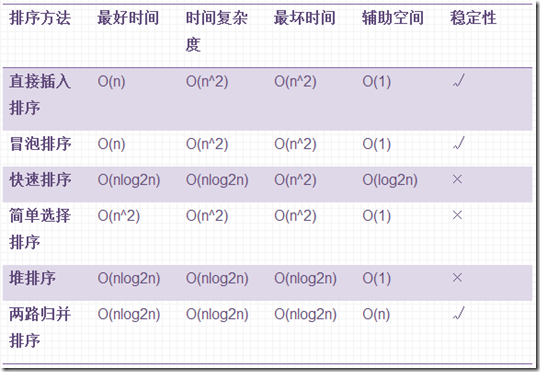
1. 从时间复杂度比较
从时间复杂度角度考虑,直接插入排序、冒泡排序、直接选择排序是三种简单的排序方法,时间复杂度均为O(n^2),而快速排序。堆排序、二路归并排序的时间复杂度都为O(nlog2n),希尔排序的时间复杂度介于这两者之间。若从最好情况的时间复杂度考虑,则直接插入排序和冒泡排序的时间复杂度最好为O(n),其他排序最好情况的时间复杂度同平均情况相同。若从最坏情况的时间复杂度考虑,则快速排序为O(n^2),直接插入排序、冒泡排序、希尔排序与平均情况的复杂度相同,但系数大约增加一倍,所以运行速度将降低一半,最坏情况对直接选择排序和归并排序影响不大。
2. 从空间复杂度比较
归并排序的空间复杂度最大,为O(n),快速排序的空间复杂度为O(log2n),其他排序的空间复杂度为O(1)。
3. 从稳定性比较
直接插入排序、冒泡排序、归并排序都是稳定的排序方法,而直接选择排序、希尔排序、快速排序、堆排序是不稳定的排序方法。
4. 从算法简单性比较
直接插入排序、冒泡排序、直接选择排序都是简单的排序方法,算法简单、易于理解,而希尔排序、快速排序、堆排序、归并排序都是改进型的排序方法,算法比简单排序要相对复杂一下。
5. 一般选择规则
(1).当待排序的记录数n不大时(n<50),可以选用直接插入排序、冒泡排序和简单选择排序中的任一种排序方法,他们的时间复杂度虽为O(n^2),但方法简单、容易实现。其中直接插入排序和冒泡排序在原记录按关键字“基本有序”时,排序速度比较快。而简单选择排序的记录交换次数较少,但是,若要求排序稳定时,不能采用简单选择排序。
(2)当待排序的记录数n较大,而对稳定性不作要求,并内存容量不宽裕时,应采用快速排序或堆排序。一般来讲,它们的排序速度较快。但快速排序对原序列基本无序的情况,时间复杂度到达O(n^2),而堆排序不会出现类似情况。
(3)当待排序记录的个数较大,内存空间允许,且要求排序稳定时,采用二路归并排序为好。
Permalink
好羡慕你们啊,能搞懂这么高深的代码!以前想学,只是没有坚持下来,最后不了了之了!
Permalink
哈哈,我也只是略懂而已~
Permalink
学长总结得很详细