广度优先搜索(Breadth-First-Search)和深度优先搜索(Deep-First-Search)是搜索策略中最经常用到的两种方法,特别常用于图的搜索.其中有很多的算法都用到了这两种思想,比如:Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
一、DFS算法
DFS的思想:
顾名思义,深度优先搜索所遵循的策略就是尽可能“深”的在图中进行搜索,对于图中某一个顶点V,如果它还有相邻的顶点(在有向图中就是还有以V为起点的边)且未被访问,则访问此顶点。如果找不到,则返回到上一个顶点。这一过程一直进行直到所有的顶点都被访问为止。 DFS可以搜索出从某一个顶点到另外的一个顶点的所有路径。 由于要进行返回的操作,我们采用的是递归的方法。
以下面的无向图为例,进行图的深度优先搜索:
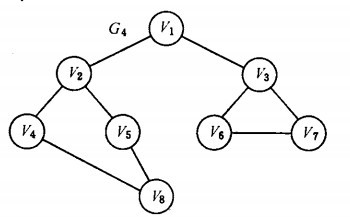
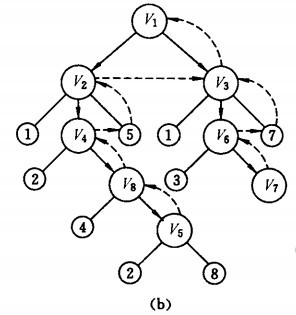
假设从顶点V1出发进行搜索,在访问了顶点V1之后,选择邻接点V2.因为V2未访问,则从V2出发进行搜索。依次类推,接着从V4、V8、V5出发进行搜索。在访问了V5之后,由于V5的邻接点都已经被访问,则搜索回到V8.由于同样的理由,搜索继续回到V4,V2直至V1,此时由于V1的另一邻接点未访问,则搜索又从V1到V3再继续进行下去。由此得到的顶点访问序列为:

显然,这是一个递归的过程。为了在遍历过程中便于区分顶点是否已被访问,需附设访问标志数组visited[0:n-1], ,其初值为FALSE ,一旦某个顶点被访问,则其相应的分量置为TRUE。
1.邻接表表示的实现方法
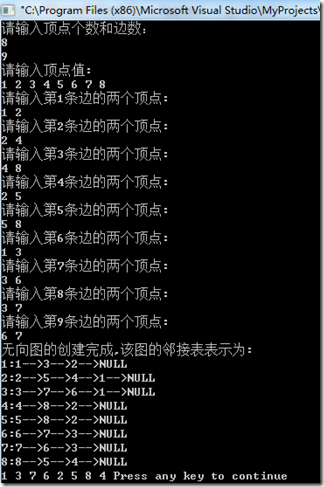
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 | //头文件 #pragma once #include <stdio.h> #include "stdlib.h" #include <iostream> using namespace std; //宏定义 #define TRUE 1 #define FALSE 0 #define NULL 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 #define INFINITY INT_MAX #define MAX_VERTEX_NUM 30 typedef int Status ; typedef int ElemType ; typedef int VrType ; typedef char VertexType ; /************************************************************************/ /* 邻接表示的图数据结构 */ /************************************************************************/ //定义边结点,即表节点 typedef struct ArcNode { int adjvex; //弧所指的顶点位置 ArcNode *nextarc; //指向下一条弧的指针 }ArcNode; //定义顶点节点,即头节点 typedef struct VNode { VertexType data; //顶点信息 ArcNode *firstarc; //指向第一条依附该顶点的弧的指针 }VNode,AdjList[MAX_VERTEX_NUM]; //定义无向图 typedef struct { AdjList vertices; int vexnum,arcnum; //图的当前顶点数和弧数 }ALGraph; //cpp文件 #include "dfs.h" bool visited[MAX_VERTEX_NUM]; //访问标识 Status (*VisitFunc) (int v); //函数变量 /************************************************************************/ /* 在无向图中添加以m,n为顶点的边 */ /************************************************************************/ void ArcAdd(ALGraph &G,int m,int n){ ArcNode *p,*h,*q; p = new ArcNode; p->adjvex = m; p->nextarc = NULL; h = q = G.vertices[n].firstarc; if(q == NULL) G.vertices[n].firstarc = p; else { if((p->adjvex)>(q->adjvex)){ p->nextarc = q; G.vertices[n].firstarc = p; } else { while( G.vertices[n].firstarc != NULL && q->nextarc != NULL && (p->adjvex)<(q->adjvex)){ //使邻接表中边的数据按大到小排列。 h = q; q = q->nextarc; } if(q->nextarc == NULL&&(p->adjvex)<(q->adjvex)){ q->nextarc = p; } else { p->nextarc = q; h->nextarc = p; } } } } /************************************************************************/ /* 创建无向图 */ /************************************************************************/ void CreateDG(ALGraph &G){ cout<<"请输入顶点个数和边数:"<<endl; cin>> G.vexnum>> G.arcnum; cout<<"请输入顶点值:"<<endl; for(int i= 1; i<= G.vexnum; i++) { char t; cin>>t; G.vertices[i].data = t; G.vertices[i].firstarc = NULL; } int m, n; for(int k = 1; k<=G.arcnum; k++){ cout<<"请输入第"<<k<<"条边的两个顶点:"<<endl; cin>>m>>n; if(m<= G.vexnum && n <= G.vexnum && m>0 && n>0){ ArcAdd(G, m, n); ArcAdd(G, n, m); } else cout<<"ERROR."<<endl; } } /************************************************************************/ /* 打印邻接表的无向图 */ /************************************************************************/ void PrintGraph(ALGraph G) { cout<<"无向图的创建完成,该图的邻接表表示为:"<<endl; ArcNode *p; for(int i=1; i<=G.vexnum; i++) { if(G.vertices[i].firstarc == NULL) cout<<i<<":"<<G.vertices[i].data<<"-->NULL"<<endl; else { p = G.vertices[i].firstarc; cout<<i<<":"<<G.vertices[i].data<<"-->"; while(p->nextarc!=NULL) { cout<<p->adjvex<<"-->"; p = p->nextarc; } cout<<p->adjvex<<"-->NULL"<<endl; } } } /************************************************************************/ /* 返回v的第一个邻接顶点。若顶点在G中没有邻接表顶点,则返回“空”。 */ /************************************************************************/ int FirstAdjVex(ALGraph G,int v) { if(G.vertices[v].firstarc) return G.vertices[v].firstarc->adjvex; else return NULL; } /************************************************************************/ /* 返回v的(相对于w的)下一个邻接顶点。若w是v的最后一个邻接点,则返回“回”。 */ /************************************************************************/ int NextAdjVex(ALGraph G,int v,int w) { ArcNode *p; if(G.vertices[v].firstarc==NULL) return NULL; else { p = G.vertices[v].firstarc; while(p->adjvex!=w) p = p->nextarc; if(p->nextarc == NULL) return NULL; else return p->nextarc->adjvex; } } void visitVex(ALGraph G, int v){ cout<<G.vertices[v].data<<" "; } /************************************************************************/ /* 无向图的深度遍历 */ /************************************************************************/ //从第v个顶点出发递归地深度优先遍历图G void DFS(ALGraph G,int v) { visited[v] = true; visitVex(G, v); for(int w = FirstAdjVex(G,v);w >= 1; w = NextAdjVex(G,v,w)) if(!visited[w]) DFS(G,w); } //对图G作深度优先遍历 void DFSTraverse(ALGraph G) { for(int v = 1; v <= G.vexnum; v++) visited[v]=false; for(int m = 1; m <= G.vexnum; m++) if(!visited[m]) DFS(G,m); } void main(){ ALGraph G; CreateDG(G); PrintGraph(G); DFSTraverse(G); } |
运行结果:
2.邻接矩阵存储方式的实现
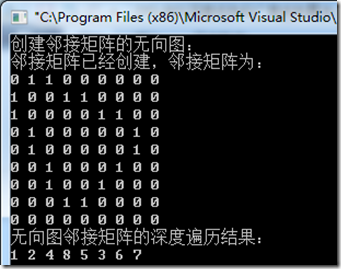
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 | //头文件 #pragma once #include <stdio.h> #include "stdlib.h" #include <iostream> using namespace std; //宏定义 #define TRUE 1 #define FALSE 0 #define NULL 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 #define INFINITY INT_MAX #define MAX_VERTEX_NUM 30 typedef int Status ; typedef int ElemType ; typedef int VrType ; typedef char VertexType ; /************************************************************************/ /* 数组表示:邻接矩阵数据结构 */ /************************************************************************/ typedef struct ArcCell{ VrType adj; //顶点关系类型,对无权图,0/1表示是否相邻,有权图表示权值 ArcCell *info; //弧相关信息的指针 }ArcCell, AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct{ VertexType vexs[MAX_VERTEX_NUM]; //顶点向量 AdjMatrix arcs; //邻接矩阵 int vexnum,arcnum; //图的当前顶点数和弧数 }MGraph; //Cpp文件 #include "dfs.h" bool visited[MAX_VERTEX_NUM]; //访问标识 Status (*VisitFunc) (int v); //函数变量 /************************************************************************/ /* 确定顶点v在图G的位置 */ /************************************************************************/ int LocateVex(MGraph G,VertexType v) { for(int i = 0; i<G.vexnum; ++i) { if(G.vexs[i] == v) return i;//找到 } return -1;//不存在 } /************************************************************************/ /* */ /************************************************************************/ int FirstAdjVex(MGraph G,int v) { int i ; for(i = 0; i<G.vexnum; i++) if( G.arcs[v][i].adj ) return i; if(i == (G.vexnum -1)) return -1; return -1; } int NextAdjVex(MGraph G,int v,int w) { int i; for( i = w+1; i<G.vexnum; i++)//+1 if(G.arcs[v][i].adj) return i; if(i == (G.vexnum -1)) return -1; return -1; } /************************************************************************/ /* 邻接矩阵的无向图的创建: 注释的代码可以动态生成图。 */ /************************************************************************/ void CreatUDG(MGraph &G){ cout<<"创建邻接矩阵的无向图:"<<endl; int i,j; //G5的存储: G.arcnum = 8; G.vexnum = 9; for(i=0;i<G.vexnum;++i) for(j=0;j<G.vexnum;++j) { G.arcs[i][j].adj=0; G.arcs[i][j].info=NULL; } G.vexs[0] = '1'; G.vexs[1] = '2'; G.vexs[2] = '3'; G.vexs[3] = '4'; G.vexs[4] = '5'; G.vexs[5] = '6'; G.vexs[6] = '7'; G.vexs[7] = '8'; G.arcs[0][1].adj = 1; G.arcs[0][1].info = NULL; G.arcs[1][0].adj = 1; G.arcs[1][0].info = NULL; G.arcs[1][3].adj = 1; G.arcs[1][3].info = NULL; G.arcs[3][1].adj = 1; G.arcs[3][1].info = NULL; G.arcs[3][7].adj = 1; G.arcs[3][7].info = NULL; G.arcs[7][3].adj = 1; G.arcs[7][3].info = NULL; G.arcs[1][4].adj = 1; G.arcs[1][4].info = NULL; G.arcs[4][1].adj = 1; G.arcs[4][1].info = NULL; G.arcs[4][7].adj = 1; G.arcs[4][7].info = NULL; G.arcs[7][4].adj = 1; G.arcs[7][4].info = NULL; G.arcs[0][2].adj = 1; G.arcs[0][2].info = NULL; G.arcs[2][0].adj = 1; G.arcs[2][0].info = NULL; G.arcs[2][5].adj = 1; G.arcs[2][5].info = NULL; G.arcs[5][2].adj = 1; G.arcs[5][2].info = NULL; G.arcs[2][6].adj = 1; G.arcs[2][6].info = NULL; G.arcs[6][2].adj = 1; G.arcs[6][2].info = NULL; G.arcs[5][6].adj = 1; G.arcs[5][6].info = NULL; G.arcs[6][5].adj = 1; G.arcs[6][5].info = NULL; return ; /* char v1,v2; cout<<"请输入无向图顶点个数和边数:"<<endl; cin>>G.vexnum>>G.arcnum; cout<<"请输入"<<G.vexnum<<"个顶点的值:"<<endl; for(i=0;i<G.vexnum;++i) cin>>G.vexs[i]; for(i=0;i<G.vexnum;++i) for(j=0;j<G.vexnum;++j) { G.arcs[i][j].adj=0; G.arcs[i][j].info=NULL; } for( k=1;k<=G.arcnum;++k){ cout<<"请输入第"<<k<<"条边的两个顶点值和它们的权重:"<<endl; cin>>v1>>v2>>w; i = LocateVex(G,v1); j=LocateVex(G,v2); G.arcs[i][j].adj=w; G.arcs[j][i]=G.arcs[i][j]; } */ } /************************************************************************/ /* 有向图邻接矩阵的创建 */ /************************************************************************/ void CreatDG(MGraph &G){ int i,j,k,w; char v1,v2; G.arcnum = 8; G.vexnum = 9; cout<<"请输入有向图顶点个数和边数:"; cin>> G.vexnum>> G.arcnum; cout<<"请输入"<<G.vexnum<<"个顶点的值:"<<endl; for(i=0;i<G.vexnum;++i) cin>>G.vexs[i]; for(i=0;i<G.vexnum;++i) for(j=0;j<G.vexnum;++j) { G.arcs[i][j].adj = 0; G.arcs[i][j].info = NULL; } for( k=1;k<=G.arcnum;++k){ cout<<"请输入第"<<k<<"条边的两个顶点值和它们的权重:"<<endl; cin>>v1>>v2>>w; i= LocateVex(G,v1); j = LocateVex(G,v2); G.arcs[i][j].adj = w; } } void visitVex(MGraph G, int v){ cout<<G.vexs[v]<<" "; } /************************************************************************/ /* 以V为出发点对图G 进行递归地DFS 搜索 */ /************************************************************************/ void DFS(MGraph G,int v){ visited[v] = true; visitVex( G, v); //访问第v 个顶点 for(int w = FirstAdjVex(G,v); w>=0; w = NextAdjVex(G,v,w)){ if(!visited[w]) DFS(G,w); //w未访问过,递归DFS搜索 } } /************************************************************************/ /* 无向图的深度遍历 */ /************************************************************************/ void DFSTraverse(MGraph G){// int v; for( v = 0; v < G.vexnum; ++v) visited[v] = false; for( v = 0; v < G.vexnum; ) if(!visited[v]) DFS( G, v); //v未访问过,从vi开始DFS搜索 ++v;//不要像书上写的那样,++v放到for语句,这样会导致多出一次访问 } void printMGraph(MGraph G){ cout<<"邻接矩阵已经创建,邻接矩阵为:"<<endl; for(int i=0;i<G.vexnum;i++){ for(int j=0;j<G.vexnum;j++) cout<<G.arcs[i][j].adj<<" "; cout<<endl; } } void main(){ MGraph G; CreatUDG(G); printMGraph(G); cout<<"无向图邻接矩阵的深度遍历结果:"<<endl; DFSTraverse(G); } |
运行结果:
二、BFS算法
从一个图的某一个顶点V0出发,首先访问和V0相邻的且未被访问过的顶点V1、V2、……Vn,然后依次访问与V1、V2……Vn相邻且未被访问的顶点。如此继续,找到所要找的顶点或者遍历完整个图。
由此可以看出,用BFS进行搜索所搜索的顶点都是按深度进行扩展的,先找到到V0距离为1的所有顶点,然后找到距离V0为2的顶点……所以BFS所搜索到的都是最短的路径。
由于要将距离V0为d(d>0)的且未被方位的点都记录起来,我们采用队列这种数据结构。队列的特点是先进先出(FIFO),从某个顶点出发,记此顶点已访问标记,然后依次搜索和此顶点相邻的且未被访问的顶点,将其加入队列,并置已访问标记,重复此步骤,直到找到需要搜索的顶点或者所有的顶点都被访问为止。
以下面的无向图为例,进行图的广度优先搜索:


首先访问v1 和v1 的邻接点v2 和v3,然后依次访问v2 的邻接点v4 和v5 及v3 的邻接点v6 和v7,最后访问v4 的邻接点v8。由于这些顶点的邻接点均已被访问,并且图中所有顶点都被访问,由些完成了图的遍历。得到的顶点访问序列为:
v1→v2 →v3 →v4→ v5→ v6→ v7 →v8
和深度优先搜索类似,在遍历的过程中也需要一个访问标志数组。并且,为了顺次访问路径长度为2、3、…的顶点,需附设队列以存储已被访问的路径长度为1、2、… 的顶点。
代码实现:
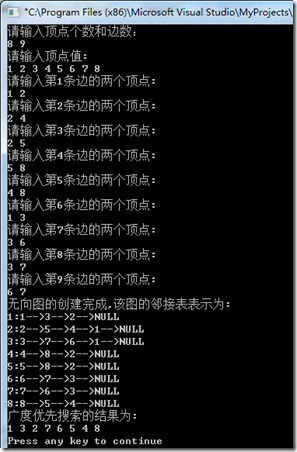
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 | //头文件 #pragma once #include <iostream> using namespace std; //宏定义 #define TRUE 1 #define FALSE 0 #define NULL 0 #define OK 1 #define ERROR 0 #define INFEASIBLE -1 #define OVERFLOW -2 #define INFINITY INT_MAX #define MAX_VERTEX_NUM 30 typedef int Status ; typedef int ElemType ; typedef int VrType ; typedef char VertexType ; /************************************************************************/ /* 邻接表示的图数据结构 */ /************************************************************************/ //定义边结点 typedef struct ArcNode { int adjvex; //弧所指的顶点位置 ArcNode *nextarc; //指向下一条弧的指针 }ArcNode; //定义顶点结点 typedef struct VNode { VertexType data; //顶点信息 ArcNode *firstarc; //指向第一条依附该顶点的弧的指针 }VNode,AdjList[MAX_VERTEX_NUM]; //定义无向图 typedef struct { AdjList vertices; int vexnum,arcnum; //图的当前顶点数和弧数 }ALGraph; /************************************************************************/ /* 需要 */ /************************************************************************/ typedef struct node //定义结点 { char data; node *next; }*Link; typedef struct //定义链表 { Link head,tail; int len; }Queue; /************************************************************************/ /* 构造一个带头结点和尾结点的空的线性链表队列Q */ /************************************************************************/ Status InitQueue(Queue &Q) { Q.head = new node; Q.head->next = Q.tail = new node; Q.tail->next = NULL; Q.len = 0; return 0; } /************************************************************************/ /* //在线性链表的队列L的结尾添加一个结点 */ /************************************************************************/ void EnQueue(Queue &Q,int e) { Link q = new node; Q.tail->next = q; Q.tail->data = e; Q.tail = q; Q.tail->next = NULL; Q.len++; } /************************************************************************/ /* 出列,并将出列的元素值用e返回 */ /************************************************************************/ void DeleteQueue(Queue &Q,int &e) { if(Q.head->next == Q.tail) { cout<<"队列为空"<<endl; e = NULL; } else { Link p,q; p = Q.head->next; q = p->next; Q.head->next = q; e = p->data; delete p; Q.len--; } } //Cpp文件 #include "bfs.h" bool visited[MAX_VERTEX_NUM]; //访问标识 Status (*VisitFunc) (int v); //函数变量 /************************************************************************/ /* 在无向图中添加以m,n为顶点的边 */ /************************************************************************/ void ArcAdd(ALGraph &G,int m,int n){ ArcNode *p,*h,*q; p = new ArcNode; p->adjvex = m; p->nextarc = NULL; h = q = G.vertices[n].firstarc; if(q == NULL) G.vertices[n].firstarc = p; else { if((p->adjvex)>(q->adjvex)){ p->nextarc = q; G.vertices[n].firstarc = p; } else { while( G.vertices[n].firstarc != NULL && q->nextarc != NULL && (p->adjvex)<(q->adjvex)){ //使邻接表中边的数据按大到小排列。 h = q; q = q->nextarc; } if(q->nextarc == NULL&&(p->adjvex)<(q->adjvex)){ q->nextarc = p; } else { p->nextarc = q; h->nextarc = p; } } } } /************************************************************************/ /* 创建无向图 */ /************************************************************************/ void CreateDG(ALGraph &G){ cout<<"请输入顶点个数和边数:"<<endl; cin>> G.vexnum>> G.arcnum; cout<<"请输入顶点值:"<<endl; for(int i= 1; i<= G.vexnum; i++) { char t; cin>>t; G.vertices[i].data = t; G.vertices[i].firstarc = NULL; } int m, n; for(int k = 1; k<=G.arcnum; k++){ cout<<"请输入第"<<k<<"条边的两个顶点:"<<endl; cin>>m>>n; if(m<= G.vexnum && n <= G.vexnum && m>0 && n>0){ ArcAdd(G, m, n); ArcAdd(G, n, m); } else cout<<"ERROR."<<endl; } } /************************************************************************/ /* 打印邻接表的无向图 */ /************************************************************************/ void PrintGraph(ALGraph G) { cout<<"无向图的创建完成,该图的邻接表表示为:"<<endl; ArcNode *p; for(int i=1; i<=G.vexnum; i++) { if(G.vertices[i].firstarc == NULL) cout<<i<<":"<<G.vertices[i].data<<"-->NULL"<<endl; else { p = G.vertices[i].firstarc; cout<<i<<":"<<G.vertices[i].data<<"-->"; while(p->nextarc!=NULL) { cout<<p->adjvex<<"-->"; p = p->nextarc; } cout<<p->adjvex<<"-->NULL"<<endl; } } } /************************************************************************/ /* 返回v的第一个邻接顶点。若顶点在G中没有邻接表顶点,则返回“空”。 */ /************************************************************************/ int FirstAdjVex(ALGraph G,int v) { if(G.vertices[v].firstarc) return G.vertices[v].firstarc->adjvex; else return NULL; } /************************************************************************/ /* 返回v的(相对于w的)下一个邻接顶点。若w是v的最后一个邻接点,则返回“回”。 */ /************************************************************************/ int NextAdjVex(ALGraph G,int v,int w) { ArcNode *p; if(G.vertices[v].firstarc==NULL) return NULL; else { p = G.vertices[v].firstarc; while(p->adjvex!=w) p = p->nextarc; if(p->nextarc == NULL) return NULL; else return p->nextarc->adjvex; } } void visitVex(ALGraph G, int v){ cout<<G.vertices[v].data<<" "; } /************************************************************************/ /* 广度优先遍历图G */ /************************************************************************/ void BFSTraverse(ALGraph G) { Queue Q; int u; for(int m=1; m<= G.vexnum; m++) visited[m] = false; InitQueue(Q);//借助辅助队列。 for(int v=1;v<=G.vexnum;v++) if(!visited[v]) { visited[v]=true; visitVex(G,v); EnQueue(Q,v); while(Q.len!=0) { DeleteQueue(Q,u); for(int w=FirstAdjVex(G,u);w>=1;w=NextAdjVex(G,u,w)) if(!visited[w]) { visited[w]=true; visitVex(G,w); EnQueue(Q,w); } } } cout<<endl; } void main(){ ALGraph G; CreateDG(G); PrintGraph(G); cout<<"广度优先搜索的结果为:"<<endl; BFSTraverse(G); } |
运行结果:
分析上述算法,每个顶点至多进一次队列。遍历图的过程实质是通过边或弧找邻接点的过程,因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,两者不同之处仅仅在于对顶点访问的顺序不同。
By:AloneMonkey