字符串匹配是我们经常遇到的问题,就是在原字符串中查找子串在原字符串中首次出现的位置。
1. Brute force.
首先我们能想到的,也是最传统的做法就是暴力搜索。
利用计数指针i和j指示主串S和模式串T中当前正待比较的字符位置,从主串S的第pos个字符起和模式的第一个字符比较,若相等,则继续逐个比较后续字符;否则从主串的下一个字符起再重新和模式的字符比较。直到模式T中的每个字符依次和主串S中的一个连续字符序列相等,则匹配成功,否则匹配失败。
匹配时间复杂度O(N*M)。
该算法的效率很低,比如说:
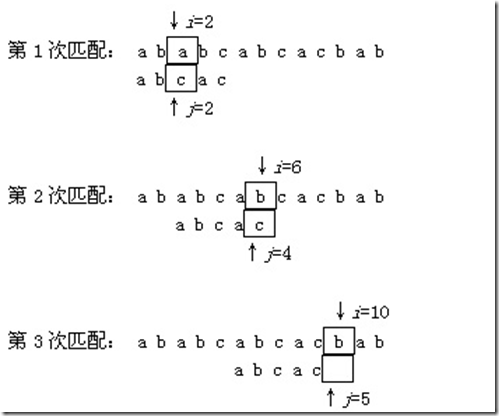
主串:ababcabcacbab
子串:abcac
我们看上面的匹配过程在第三趟的匹配中,当i=6、j=4字符比较不相等时,又要从i=3,j=1重新开始比较。但是我们仔细观察可以发现,在i=3和j=1,i=4和j=1以及i=5和j=1这3次比较都是不必进行的。因为从第三趟部分匹配的结果就可得出,主串中第4、5和6个字符必然是b、c和a(即模式串中第2、3和4个字符)。因为模式中的第一个字符是a,因此它无需再和这3个字符进行比较,而仅需将模式向右移动3个字符的位置继续进行i=6、j=1时的字符比较即可。
所以就有了KMP算法。
2. KMP算法
KMP算法解决的问题是字符匹配,是由Knuth–Morris–Pratt共同开发出来的,这个算法把字符匹配的时间复杂度缩小到O(m+n),而空间复杂度也只有O(m),n是target的长度,m是pattern的长度。
相比蛮力算法,KMP 算法预先计算出了一个哈希表,用来指导在匹配过程中匹配失败后尝试下次匹配的起始位置,以此避免重复的读入和匹配过程。这个哈希表被叫做“部分匹配值表(Particial match table)”,它的设计是算法精妙之处。
部分匹配值表
要理解部分匹配值表,就得先了解字符串的前缀(prefix)和后缀(postfix)。
- 前缀:除字符串最后一个字符以外的所有头部串的组合。
- 后缀:除字符串第一个字符以外的所有尾部串的组合。
- 部分匹配值:一个字符串的前缀和后缀中最长共有元素的长度。
举例说明:字符串ABCAB
- 前缀:{A, AB, ABC, ABCA}
- 后缀:{BCAB, CAB, AB, B}
- 部分匹配值:2 (AB)
而所谓的部分匹配值表,则为模式串的所有前缀以及其本身的部分匹配值。
举例如下:还是针对字符串ABCAB,它的部分匹配值表为:
A B C A B
0 0 0 1 2
这代表着:字符串ABCAB 中,子串ABC的部分匹配值为 0,而子串ABCA的部分匹配值为 1,诸如此理。
我们来看看next函数的定义:
- ①:next[j]=0 当j=1时
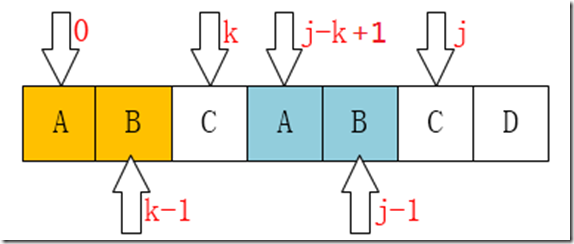
- ②:next[j] = Max{k|1<k<j,且’p1….pk-1’==pj-k+1…pj-1′} 当此集合不空时
- ③:next[j]=1 其它情况
第一种和第三种情况就不用说了,我们来看看第二种:
其实我们需要的是找出最大的K值。在满足p1….pk-1 == pj-k+1…pj-1的前提下。
简单的来说:就是求出一个字符串的前缀和后缀中最长共有元素的长度。
我们来看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | void getNext(SString T, int next[ ]) { //求模式串T的next函数值并存入数组next。 i = 1; next[1] = 0; j = 0; while(i < T[0]){ //T[0]为T的长度 if(j == 0 || T[i] == T[j]) { ++i; ++j; next[i] = j; } else j = next[j]; } } |
但是,前面定义的next函数在某些情况下还是有缺陷。例如模式 aaaab 在和主串 aabaaaab匹配时,当i=4、j=4时s.ch[4] != t.ch[4],由next[j]的指示还需进行i=4、j=3,i=4、j=2,i=4、j=1这3次比较。实际上,因为模式中第1、2、3个字符和第4个字符都相等,因此不需要再和主串中第4个字符想比较,直接进行i=5、j=1时的字符比较。这就是说,若按上述定义得到next[j] = k,而模式中Pj = Pk,则当主串中字符Si和Pj比较不等时,不需要再和Pk进行比较,而直接和Pnext[k]进行比较,换句话说,此时的next[j]应和next[k]相同。
j 1 2 3 4 5
模式 a a a a b
next[j] 0 1 2 3 4
nextval[j] 0 0 0 0 4
next函数的修正算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | void getNextVal(SString T, int nextval[ ]) { //求模式串T的next函数值并存入数组next。 i = 1; next[1] = 0; j = 0; while(i < T[0]){ if(j == 0 || T[i] == T[j]) { ++i; ++j; if(T[i] != T[j]) next[i] = j; else nextval[i] = nextval[j]; } else j = next[j]; } } |
求出了next数组了,KMP算法也就不在话下了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | //int kmp_seach(char const*, int, char const*, int, int const*, int pos) KMP模式匹配函数 //输入:src, slen主串 //输入:patn, plen模式串 //输入:nextval KMP算法中的next函数值数组 int kmp_search(char const* src, int slen, char const* patn, int plen, int const* nextval, int pos) { int i = pos; int j = 0; while ( i < slen && j < plen ) { if( j == 0 || src[i] == patn[j] ) { ++i; ++j; } else { j = nextval[j]; } } if( j >= plen ) return i-plen; else return -1; } |
本文链接:http://www.alonemonkey.com/knuth-morris-pratt-algorithm.html