最小生成树–Prim算法和Kruskal算法

一、最小生成树的概念

生成树：所有顶点均由边连接在一起，但不存在回路的图叫该图的生成树。

一个图可以有许多棵不同的生成树。

所有生成树具有以下共同特点：

生成树的顶点个数与图的顶点个数相同

生成树是图的极小连通子图

 

最小生成树：生成树的每条边上的权值之和最小。

构成最小生成树可以有多种算法。其中多数算法利用了最小生成树的下列一种简称为MST的性质：假设N=(V,{E})是一个连通图，U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值(代价)的边，其中u∈U，v∈V-U，则必存在一棵包含边(u,v)的最小生成树。

 

普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法是两个利用MST性质构造最小生成树的算法。

 

二、Prim算法

假设N=(V,{E})是连通网，TE是N上最小生成树中边的集合。

①：算法从U={u0}(u0∈V),TE={}开始。

②：在所有u∈U,v∈V-U的边(u,v)∈E中找一条代价最小的边(u0,v0)

③：(u0,v0)并入集合TE，同时v0并入U

④：重复②和③，直到U=V为止。此时TE中必有n-1条边，则T=(V,{TE})为N的最小生成树。

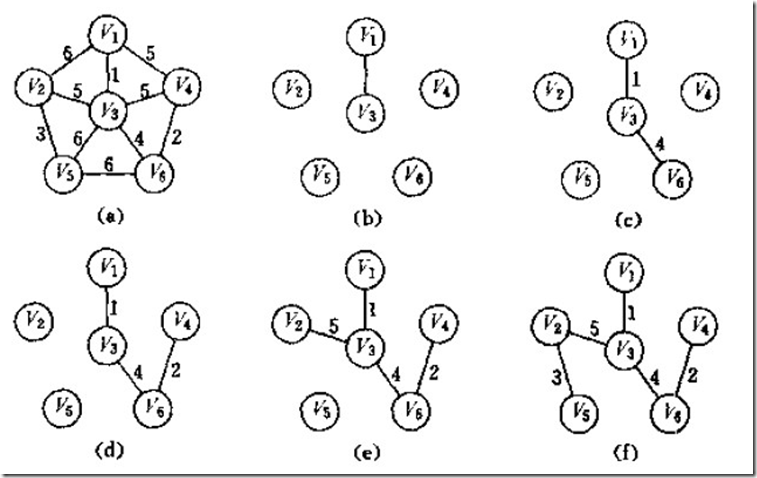
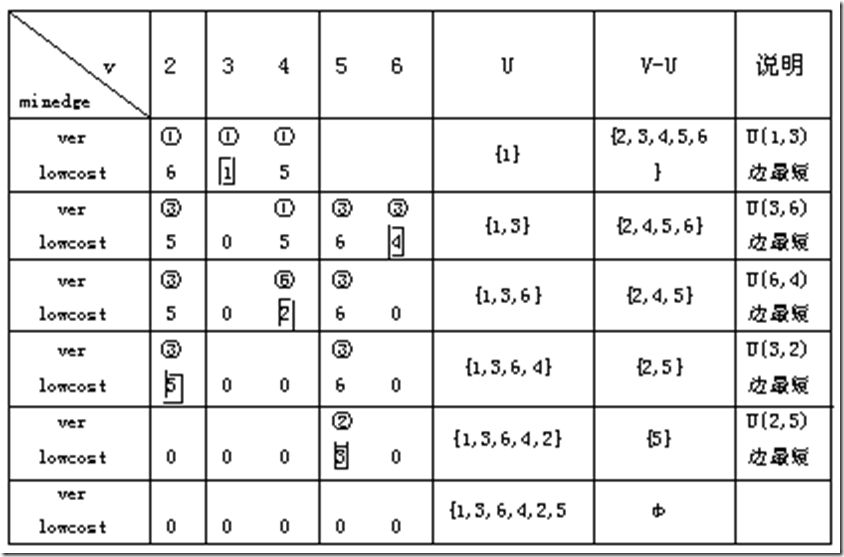
为实现这个算法需要附设一个辅助数组closedge，以记录从U到V-U具有最小代价的边，对每个顶点ui∈V-U，在辅助数组中存在一个相应分量closedge[i-1]，它包括两个域，其中lowcost存储该边上的权。显然，

closedge[i-1].lowcost = Min{cost(u,vi) | u∈U}

image

vex域存储该边依附在U中的顶点。上图为按Prim算法构造网的一棵最小生成树，在构造过程中辅助数组中各分量值的变化如下：

image

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
#include <iostream>
#include <fstream>
using namespace std;

ifstream fin("prim.txt");

#define MAX_VERTEX_NUM 20
#define ERROR -1
#define INFINITY 0x7fff


//图的邻接矩阵存储结构
typedef struct {
    char *vexs;
    int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
    int vexnum, arcnum;
}Graph;

//记录从顶点集U到V-U的代价最小的边的辅助数组定义：
typedef struct {
    char   adjvex;
    int    lowcost;
}closedge;

//图G中查找顶点c的位置
int LocateVex(Graph G, char c) {
    for(int i = 0; i < G.vexnum; ++i) {
        if(G.vexs[i] ==  c) return i;
    }
    return ERROR;
}
 
int minimum(closedge cs[MAX_VERTEX_NUM]);

//创建无向网
void CreateUDN(Graph &G){
    //采用数组（邻接矩阵）表示法，构造无向网G
    fin >> G.vexnum >> G.arcnum;
    G.vexs = (char *) malloc((G.vexnum+1) * sizeof(char));  //需要开辟多一个空间存储'/0'
    //构造顶点向量
    for(int i = 0; i < G.vexnum; i++)
        fin >> G.vexs[i];
    G.vexs[G.vexnum] = '\0';
   
    //初始化邻接矩阵
    for(i = 0; i < G.vexnum; ++i)
        for( int j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = INFINITY;  
   
    char a, b;
    int s1, s2, w;
    for(i = 0; i < G.arcnum; ++i) {
        fin >> a >> b >> w;  //输入依附于弧的权值
        s1 = LocateVex(G,a);  //找到a和b在顶点向量中的位置
        s2 = LocateVex(G,b);  
        G.arcs[s1][s2] = G.arcs[s2][s1] = w;
    }
}

class myerr{};

void MiniSpanTree_PRIN(Graph G, char u) {
    //用普里姆算法从第u个顶点出发构造网G的最小生成树T,输出T的各条边
    closedge cl[MAX_VERTEX_NUM];
    int k = LocateVex(G,u);  //返回顶点u在图G中的位置
    for(int j = 0; j < G.vexnum; ++j) { //辅助数组初始化
        if(j != k) {
            cl[j].adjvex = u;
            cl[j].lowcost = G.arcs[k][j];
        }
    }
    cl[j].adjvex = '\0';
    cl[j].lowcost = INFINITY;
    cl[k].adjvex = u; //初始，U = {u}
    cl[k].lowcost = 0;  

    for(int i = 1; i < G.vexnum; ++i) {  //此处更改！！！！ 只需运行G.vexnum-1次即可
        k = minimum(cl);  //求出T的下一个结点：第k顶点
        if (k==-1) throw myerr(); //如果明明没搜索完，minimum函数却返回-1，那么肯定出问题了，抛个异常玩玩
        cout << cl[k].adjvex << "连接" << G.vexs[k] << endl; //输出生成树的边  
        cl[k].lowcost = 0;  //第k顶点并入U集
       
        for(j = 0; j < G.vexnum; ++j)
            if(G.arcs[k][j] < cl[j].lowcost) { //新顶点并入U后重新选择最小边，将所有变化的值都更新
                cl[j].adjvex = G.vexs[k];
                cl[j].lowcost = G.arcs[k][j];
            }
    }
} //MiniSpanTree

/*
算法简要：
1、找到开始的结点
2、对辅助数组初始化
3、更新变化每一步，使得每次都选择最小边
4、调整结束
*/

int minimum(closedge cs[MAX_VERTEX_NUM]) {
    int i = 0, j = -1, min;
    min = INFINITY;
    while(cs[i].adjvex) {
        if(cs[i].lowcost < min && cs[i].lowcost != 0) { //确保已经选择过的顶点不会再被选择
            min = cs[i].lowcost;
            j = i;
        }
        i++;
    }
    return j;
}

//主函数
void main(){
    Graph G;
    CreateUDN(G);
    cout << "result:" << endl;
    MiniSpanTree_PRIN(G,'A');
    cout << endl;
}

prim.txt中的输入信息为：

6 10
A
B
C
D
E
F
A B 6
A C 1
A D 5
B C 5
B E 3
C D 5
C F 4
C E 6
D F 2
E F 6

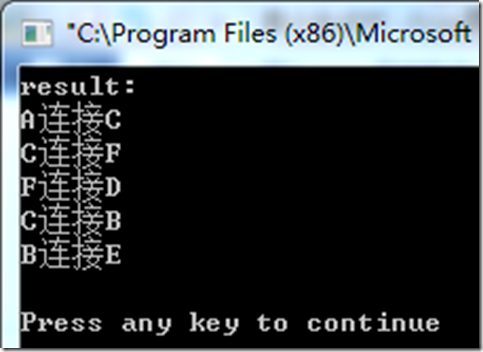
运行结果：

image

 

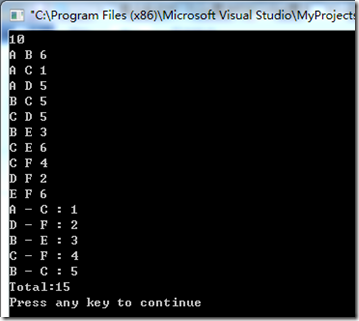
三、Kruskal算法

Prim算法时间复杂度为O(n平方)，与网中的边数无关，因此适用于求边稠密的网的最小生成树。

而克鲁斯卡尔算法恰恰相反，它的时间复杂度为O(eloge)(e为网中边的数目)，因此它相对于普里姆算法而言，适合于求边稀疏的网的最小生成树。

假设连通网N=(V,{E}),则令最小生成树：

①：初始状态为只有n个顶点而无边的非连通图T=(V,{}),图中每个顶点自成一个连通分量。

②：在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。

③：以此类推，直到T中所有顶点都在同一连通分量上为止。

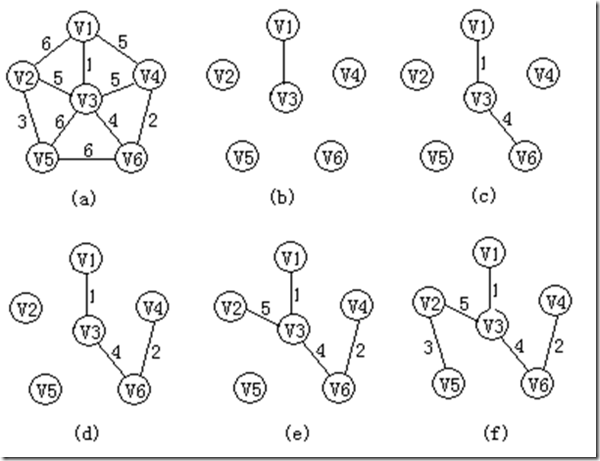
下图为依照克鲁斯卡尔算法构造一棵最小生成树的过程：

image

代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
#include <stdio.h>
#include <stdlib.h>
 
#define MAX 100
 
/* 定义边(x,y)，权为w */
typedef struct
{
    int x, y;
    int w;
}edge;
 
edge e[MAX];
/* rank[x]表示x的秩 */
int rank[MAX];
/* father[x]表示x的父节点 */
int father[MAX];
int sum;
 
/* 比较函数，按权值(相同则按x坐标)非降序排序 */
int cmp(const void *a, const void *b)
{
    if ((*(edge *)a).w == (*(edge *)b).w)
    {
        return (*(edge *)a).x - (*(edge *)b).x;
    }
    return (*(edge *)a).w - (*(edge *)b).w;
}
 
/* 初始化集合 */
void Make_Set(int x)
{
    father[x] = x;
    rank[x] = 0;
}
 
/* 查找x元素所在的集合,回溯时压缩路径 */
int Find_Set(int x)
{
    if (x != father[x])
    {
        father[x] = Find_Set(father[x]);
    }
    return father[x];
}
 
/* 合并x,y所在的集合 */
void Union(int x, int y, int w)
{
 
    if (x == y) return;
    /* 将秩较小的树连接到秩较大的树后 */
    if (rank[x] > rank[y])
    {
        father[y] = x;
    }
    else
    {
        if (rank[x] == rank[y])
        {
            rank[y]++;
        }
        father[x] = y;
    }
    sum += w;
}
 
/* 主函数 */
int main()
{
    int i, n;
    int x, y;
    char chx, chy;
 
    /* 读取边的数目 */
    scanf("%d", &n);
    getchar();
 
    /* 读取边信息并初始化集合 */
    for (i = 0; i < n; i++)
    {
        scanf("%c %c %d", &chx, &chy, &e[i].w);
        getchar();
        e[i].x = chx - 'A';
        e[i].y = chy - 'A';
        Make_Set(i);
    }
 
    /* 将边排序 */
    qsort(e, n, sizeof(edge), cmp);
 
    sum = 0;
 
    for (i = 0; i < n; i++)
    {
        x = Find_Set(e[i].x);
        y = Find_Set(e[i].y);
        if (x != y)
        {
            printf("%c - %c : %d\n", e[i].x + 'A', e[i].y + 'A', e[i].w);
            Union(x, y, e[i].w);
        }
    }
 
    printf("Total:%d\n", sum);
    //system("pause");
    return 0;  
}

运行结果：

image

本文链接：http://www.alonemonkey.com/prim-and-kruskal.html